Representing primes in binary quadratic forms

Introduction

Prime numbers are of great importance in mathematics. An integer \(p\) is called prime if the only divisors are \(1\) and \(p\). There was always a curiosity about the patterns which can be found in prime numbers. There are sequences of numbers like even numbers, triangular numbers whose \(n^{\text{th}} \) can be easily predicted. For example  \(n^{\text{th}} \) triangular number is given by the formula

$$ \frac{n(n+1)}{2}$$

There are also other sequences like Fibonacci numbers whose  \(n^{\text{th}} \) is given by the formula 

$$ F_n = F_{n-1} + F_{n-2}$$ with \( F_1=F_0=1\).

It turns out that no nice formula for  \(n^{\text{th}} \) prime number is known. So people started looking out for other patterns. In  1640, Fermat wrote a letter to Mersenne in which he mentions "Every prime number which surpasses by one a multiple of four is composed of two squares. Examples are 5, 13, 17, 29, 37, 41, etc." Formally for any  prime  \( p \) $$ p =x^2 +y^2 \iff p \equiv 1 \pmod 4$$ for some integers \(x,y\). Even though Fermat did not provide the proof of this claim, Euler managed to give one.

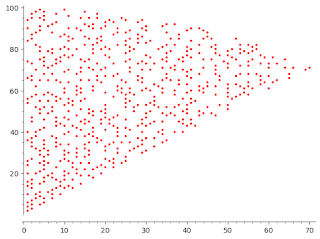\((x,y)\) such that \(x<y\) and  \(x^2+y^2\) a is prime below 10000

We will try to prove the above claim using quadratic residues and PIDs. 

Theorem 

 Let \(m \) be a non square integer such that \( \mathbb{Z}[\sqrt m] \) is a principal ideal domain. Let \( p\) be an odd prime such that $$(m \mid p) = 1$$. Then there exist integers \(u,v\) such that $$p = \pm(u^2-mv^2)$$

Proof:

We just give an outline of the proof and dillegent reader should fill the gaps. Since \( (m \mid p) =1 \) there exist \( x\) such that $$ x^2 \equiv m \pmod p$$ so \( p \mid (x- \sqrt m) (x + \sqrt m)\) but \( p \nmid (x \pm \sqrt m )\). So \( p \) is not a prime in  \( \mathbb{Z}[\sqrt m] \). Since  \( \mathbb{Z}[\sqrt m] \) is a PID, \(p\) is reducible. So there exist integers \(u,v,a,\) and \(b\) such that $$ p  = (u+ v\sqrt m)(a + b\sqrt m)$$ where  \( u+ v\sqrt m\) and \( a + b\sqrt m \)  are not units.

It can be easily seen that $$ p^2 = (u^2 -mv^2)(a^2-mb^2)$$ It follows that $$p = \mid u^2 -mv^2 \mid = \mid  a^2 -mb^2 \mid $$ which is sufficient to conclude.

Application of the previous theorem

It is known that when \(m\) is a negative squarefree integer \( \mathbb{Z}[\sqrt m] \) is a PID only if \(m = -1,-2,-3,-7,-11,-19,-43,-67,-163\). We limit our discussion for the case \( m=-1,-2\).

It is known that for a prime \(p\), $$ (-1 \mid p) =1 \iff  p \equiv 1 \pmod 4$$ so this gives Fermat's theorem.

Also $$  (-2 \mid p) = 1 \iff p \equiv 1,3 \pmod 8 $$ so it follows that $$p =x^2+2y^2 \iff  p \equiv 1,3 \pmod 8 $$ 

The limitation of the theorem is that we do not know the complete list of \(m\) such that \( \mathbb{Z}[\sqrt m] \) is PID for \(m >0\). This theorem can not be easily extended to cubic domains and above since cubic residues are not as simple as quadratic residues.